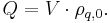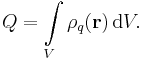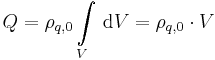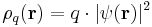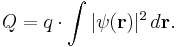Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter (C/m), square meter (C/m²), or cubic meter (C/m³), respectively, and represented by the lowercase Greek letter Rho (ρ). Since there are positive as well as negative charges, the charge density can take on negative values. Like any density it can depend on position. It should not be confused with the charge carrier density. As related to chemistry, it can refer to the charge distribution over the volume of a particle, molecule, or atom. Therefore, a lithium cation will carry a higher charge density than a sodium cation due to its smaller ionic radius.
Contents |
Classical charge density
Continuous charges
The integral of the charge density 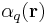 ,
, 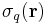 ,
, 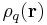 over a line
over a line 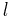 , surface
, surface  , or volume
, or volume  , is equal to the total charge
, is equal to the total charge  of that region, defined to be:[1]
of that region, defined to be:[1]
This relation defines the charge density mathematically. Note that the symbols used to denote the various dimensions of charge density vary between fields of studies. Other commonly used notations are  ,
,  ,
,  ; or
; or 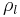 ,
, 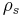 ,
, 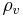 for (C/m), (C/m²), (C/m³), respectively.
for (C/m), (C/m²), (C/m³), respectively.
Homogeneous charge density
For the special case of a homogeneous charge density, that is one that is independent of position, equal to 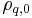 the equation simplifies to:
the equation simplifies to:
The proof of this is simple. Start with the definition of the charge of any volume:
Then, by definition of homogeneity, 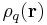 is a constant that we will denote
is a constant that we will denote 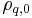 to differentiate between the constant and non-constant forms, and thus by the properties of an integral can be pulled outside of the integral resulting in:
to differentiate between the constant and non-constant forms, and thus by the properties of an integral can be pulled outside of the integral resulting in:
so,
The equivalent proofs for linear charge density and surface charge density follow the same arguments as above.
Discrete charges
If the charge in a region consists of  discrete point-like charge carriers like electrons the charge density can be expressed via the Dirac delta function, for example, the volume charge density is:
discrete point-like charge carriers like electrons the charge density can be expressed via the Dirac delta function, for example, the volume charge density is:
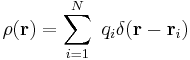 ;
;
where 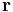 is the test position,
is the test position,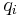 is the charge of the ith charge carrier, whose position is
is the charge of the ith charge carrier, whose position is 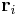 .
.
If all charge carriers have the same charge  (for electrons
(for electrons 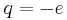 ) the charge density can be expressed through the charge carrier density
) the charge density can be expressed through the charge carrier density 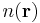 : Again, the equivalent equations for the linear and surface charge densities follow directly from the above relations.
: Again, the equivalent equations for the linear and surface charge densities follow directly from the above relations.
Relative charge density
From the perspective of the theory of relativity, the length of a segment of wire depends on velocity of observer, so charge density is a relative concept. Anthony French[2] has described how the magnetic field force of a current-bearing wire arises from this relative charge density. He used (p 260) a Minkowski diagram to show "how a neutral current-bearing wire appears to carry a net charge density as observed in a moving frame." The approach to electromagnetism through spacetime symmetry is called relativistic electromagnetism.
Quantum charge density
In quantum mechanics, charge density is related to wavefunction 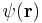 by the equation
by the equation
when the wavefunction is normalized as
Application
The charge density appears in the continuity equation, which follows from Maxwell's Equations in the electromagnetic theory.
See also
- Continuity equation relating charge density and current density
- Ionic potential
References
- ^ Spacial Charge Distributions - http://faculty.wwu.edu/vawter/PhysicsNet/Topics/Gauss/SpacialCharge.html
- ^ A. French (1968) Special Relativity, chapter 8 Relativity and electricity, pp 229–65, W. W. Norton.
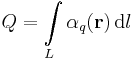 (
(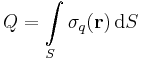 (
(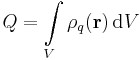 (
(